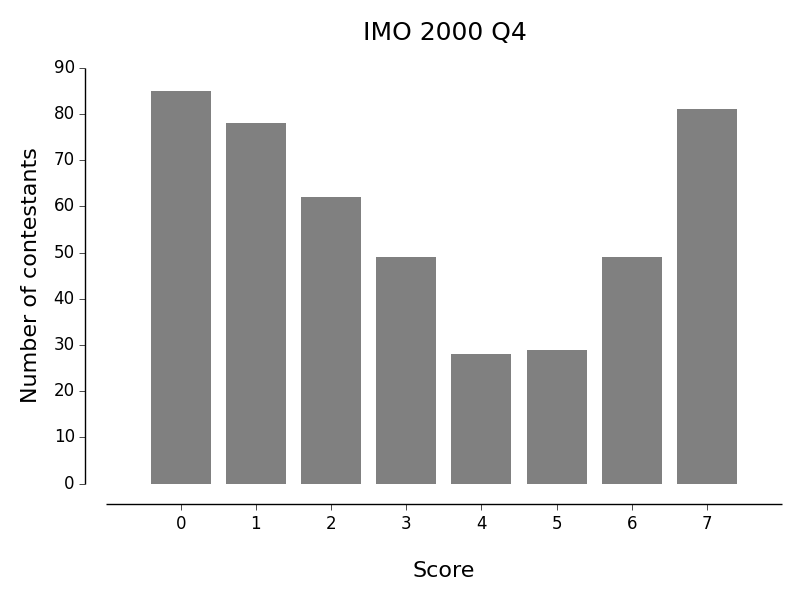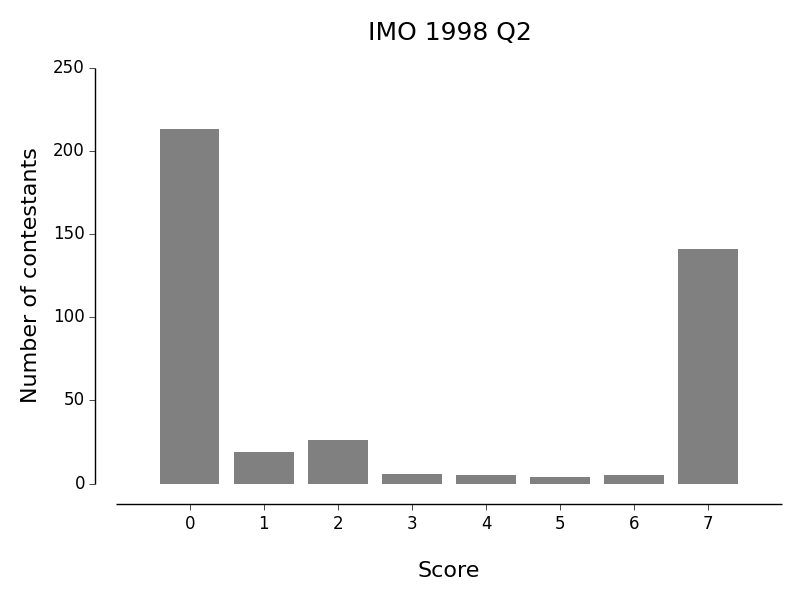

As an experiment then, I picked some old problems from the International Mathematical Olympiad as well a simple result from finite group theory, each with what I felt had the right combinatorial flavour.
It was fun playing with these problems but in the end I didn't really feel that I had achieved my goal. On the plus side, I was a little surprised at the usefulness of one observation. It hints at the sort of thing I'd like to find so for what it's worth here it is:
When the data for a combinatorial problem can be regarded as a finite subset of a product \( S \subseteq X\times Y\), the trivial observation that the size of \(S\) can be regarded as the sum of the sizes its fibres over both the natural map to \(X\) as well as the natural map to \(Y\) can reveal apparently-tricky counting arguments to be trivial.In other words, in terms of the diagram: $$ X \xleftarrow{\mu} S \xrightarrow{\nu} Y $$ intuition sometimes fails to capture the trivial statement that: $$ \sum_{x\in X}\|\mu^{-1}(x)\| = \sum_{y\in Y}\|\nu^{-1}(y)\| $$ (Note that I am not assuming \(\mu, \nu\) are invertible; the above notation indicates set preimages.) I'll refer to this as the double-counting trick below. It is just the statement that you may count the edges of a bipartite graph grouping by either set of nodes.
In a competition, there are \(a\) contestants and \(b\) judges, where \(b \ge 3\) is an odd integer. Each judge rates each contestant as either "pass" or "fail". Suppose \(k\) is a number such that, for any two judges, their ratings coincide for at most \(k\) contestants. Prove that \(k/a \ge (b - 1)/(2b) \).
Twenty-one girls and twenty-one boys took part in a mathematical contest.Prove that there was a problem that was solved by at least three girls and at least three boys.
- Each contestant solved at most six problems.
- For each girl and each boy, at least one problem was solved by both of them.
In a mathematical competition, in which 6 problems were posed to the participants, every two of these problems were solved by more than \(\frac{2}{5}\) of the contestants. Moreover, no contestant solved all the 6 problems. Show that there are at least 2 contestants who solved exactly 5 problems each.
Suppose that a finite group \(G\) acts on a finite set \(X\) then: $$ \|X/G\| = \frac{1}{\|G\|}\sum_{g\in G}\|Fix(g)\| $$ where \(Fix(g) = \{x\in X~|~g\cdot x = x\}\).

So those are the test cases. If you like this sort of thing and are lucky enough to be possessed of 20 minutes as well as extraordinary will power, I'd suggest resisting the temptation to read on before spending about 10 minutes on each of the first two.
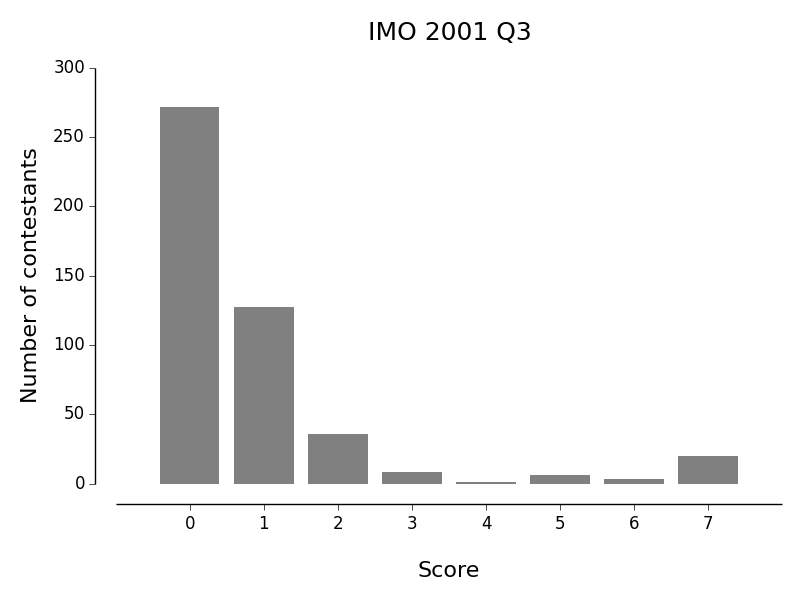
The point is, that was all totally mechanical. Now look back at the histogram of results!
Incidentally there's a pleasing interpretation of this result in terms of graph theory. We take the complete bipartite graph whose two sets of nodes are contestants and judges and colour an edge white or black according to whether the judge rated a contestant pass or fail.
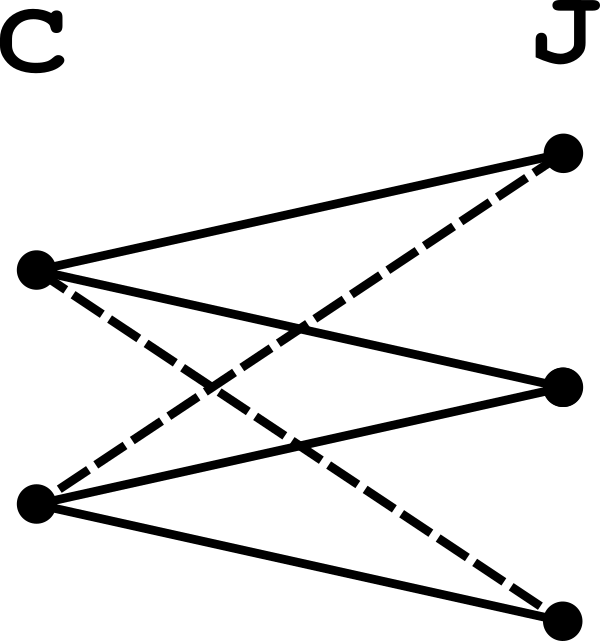
\(a\) girls and \(a\) boys took part in a mathematical contest.Prove there was a problem that was solved by \(x\) boys and \(x\) girls, where \(x = \left\lceil\frac{a}{2(n-1)}\right\rceil\).
- Each contestant solved at most \(n\) problems (\(n > 1\)).
- For each girl and each boy, at least one problem was solved by both of them.
Let \(G, B, P\) be the sets of girls, boys and problems and let: $$ P(l, G) = \{p \in P ~|~ \mbox{at least $l$ girls solved $p$}\} $$ and similarly for \(P(l, B)\). The problem asks us to establish a lower bound for: $$ k = \max\{l \in \mathbb{N} ~|~ P(l, G) \cap P(l, B) \ne \emptyset \} $$
The data supplied in the problem is a subset \(S \subseteq (G\sqcup B)\times P\). Let $$ S(G, B) = \{ (g, b, p) \in G\times B\times P ~|~ (g, p) \in S, (b, p) \in S\} $$ and note that there are natural maps: $$ G\times B \xleftarrow{\mu_{G,B}} S(G, B) \xrightarrow{\nu_{G,B}} P $$ Similarly define \(S(G) \subseteq G\times P\) and \(S(B) \subseteq B\times P\) and note that these all fit into the commutative diagram:
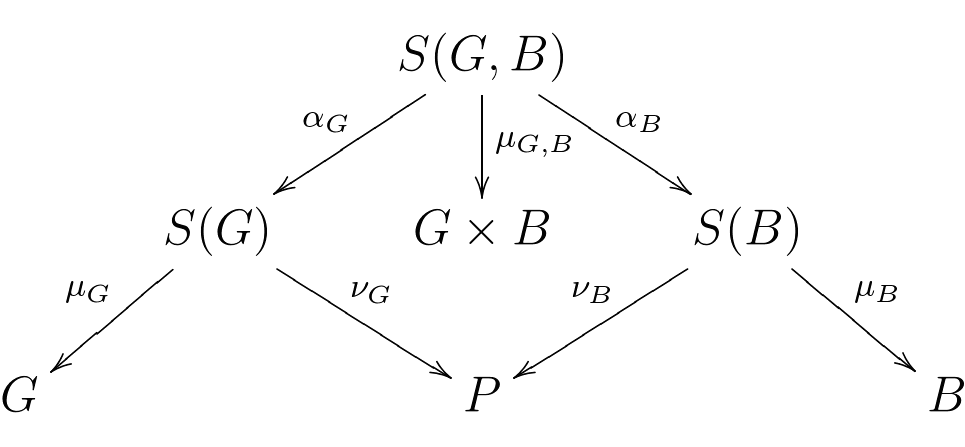
We've done nothing so far, so how should we begin? We use the double-counting trick for \(S(G, B)\) of course! Because \(\mu_{G,B}\) is surjective we have: $$ a^2 \le \|S(G, B)\| = \sum_{p\in P}\|\nu_{G,B}^{-1}(p)\| $$ Bearing in mind the definition of \(k\), it is natural to split this sum up into the fibres over \(P(k+1, G)\) and its complement and to use the two different factorisations of \(\nu_{G,B}\) to get: $$ \begin{align} a^2 &\le \sum_{p\in P(k+1, G)}\|\alpha_G^{-1}(\nu_G^{-1}(p))\| + \sum_{p \notin P(k+1, G)}\|\alpha_B^{-1}(\nu_B^{-1}(p))\|\\ &\le k\sum_{p\in P(k+1, G)}\|\nu_G^{-1}(p)\| + k\sum_{p \notin P(k+1, G)}\|\nu_B^{-1}(p)\| \end{align} $$ by definition of \(k\) for the first term and by definition of \(P(k+1, G)\) for the second. So we have: $$ a^2 \le k\left(\|\nu_G^{-1}(P(k+1, G))\| + \|\nu_B^{-1}(P(k+1, G)')\|\right) $$ OK that was easy but how do we deal with these terms? We just use the double-counting trick twice more of course: once each for \(S(G)\) and \(S(B)\). For \(S(G)\) it yields: $$ \|\nu_G^{-1}(P(k+1, G))\| + \|\nu_G^{-1}(P(k+1, G)')\| = \|S(G)\| \le na $$ Obviously we can only make progress if we can say something about \(\nu_G^{-1}(P(k+1, G)')\).
As far as I can see, this is the one point at which we actually need to think. Focus attention on one girl. She solved at most \(n\) problems and yet solved at least one problem in common with each of the \(a\) boys. By the pigeon hole principle, one of the problems she solved was solved by at least \(\lceil a/n\rceil\) boys. In other words: $$ \mu_G(\nu_G^{-1}(P(\lceil a/n\rceil, B))) = G $$ and so: $$ \|\nu_G^{-1}(P(\lceil a/n\rceil, B))\| \ge \|G\| = a $$ Since \(\lceil a/n\rceil \ge \lceil a/(2(n-1))\rceil\) we can assume \(k < \lceil a/n\rceil\) without loss of generality and so \(P(k+1, G) \cap P(\lceil a/n\rceil, B) = \emptyset\) by definition of \(k\), or in other words \(P(\lceil a/n\rceil, B) \subseteq P(k+1, G)'\). Thus by our pigeon-hole-principle result above we get: $$ \|\nu_G^{-1}(P(k+1, G)')\| \ge a $$ and so combining this with the result of our double-counting argument for \(S(G)\) we have: $$ \|\nu_G^{-1}(P(k+1, G))\| \le (n-1)a $$ A similar argument for \(S(B)\) yields: $$ \|\nu_B^{-1}(P(k+1, G)')\| \le (n-1)a $$ Combining results we thus have: $$ a^2 \le 2k(n-1)a $$ and the problem is solved.
Like its predecessor, there is a natural graph-theoretic interpretation of this problem; we take a graph with three sets of nodes: boys, girls, and problems with an edge joining each contestant to the problems they solved.
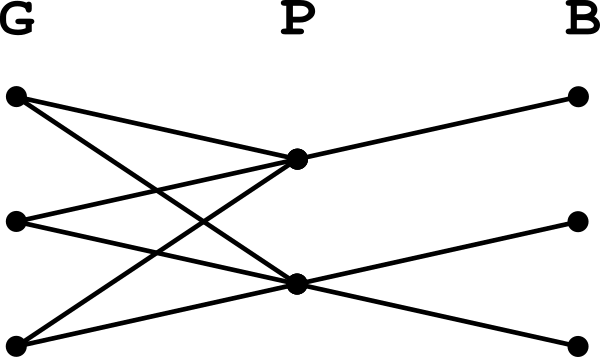
Incidentally the above proof generalises easily to the case that there are unequal numbers of girls and boys. For example if there are \(g\) girls, each of whom solved at most \(n\) problems and \(b\) boys each of whom solved at most \(m\) problems and if \(b+g \le \min(ng, mb)\) then there must exist a problem solved by at least \(x\) girls and \(x\) boys where: $$ x = \left\lceil\frac{gb}{(n-1)g + (m-1)b}\right\rceil. $$ Update 2019-07-06: see here for a much simpler solution to this problem.
Let \(C\) be the set of contestants and \(P\) the set of problems. Because of the \(\frac{2}{5}\) constraint, we want counts involving problem pairs. Thus let \(P^{(2)} = \{ \{p, q\} ~|~ p, q \in P, p \ne q \}\) be the 15-element set of unordered problem pairs.
The data of who solved which problem pairs gives us a subset \(S \subseteq C\times P^{(2)}\) and thus natural maps: $$ C \xleftarrow{\mu} S \xrightarrow{\nu} P^{(2)} $$ We mechanically apply the double counting technique. From the map \(\mu\) we obtain $$ \|S\| = C_2 + 3C_3 + 6C_4 + 10C_5, $$ where \(C_i\) is the number of contestants who solved exactly \(i\) problems (and we have used the fact that \(C_6 = 0\)). From the map \(\nu\) we obtain $$ \begin{align} \|S\| &= \sum_{x\in P^{(2)}} \|\nu^{-1}(x)\|\\ &\ge \|P^{(2)}\|\min_{x\in P^{(2)}} \|\nu^{-1}(x)\|\\ &= 15\min_{x\in P^{(2)}} \|\nu^{-1}(x)\|. \end{align} $$ We're given: $$ \min_{x\in P^{(2)}} \|\nu^{-1}(x)\| > \frac{2}{5}\|C\|, $$ and so because of integrality: $$ \min_{x\in P^{(2)}} \|\nu^{-1}(x)\| \ge \left\lfloor\frac{2}{5}\|C\|\right\rfloor + 1 \ge \frac{2\|C\| + 1}{5}. $$ The double-counting trick thus yields: $$ C_2 + 3C_3 + 6C_4 + 10C_5 \ge 15\cdot\frac{2(C_1 + C_2 + C_3 + C_4 + C_5) + 1}{5}. $$ This rearranges to: $$ 4C_5 \ge 6C_1 + 5C_2 + 3C_3 + 3, $$ which requires \(C_5 \ge 1\). We proceed by assuming \(C_5 = 1\) and obtaining a contradiction. By the above inequality we necessarily have \(C_1 = C_2 = C_3 = 0\). So we are considering the case that all contestants solved 4 problems except for one who solved 5 problems, and who we will denote by: $$ \hat c \in C. $$
Further, we will denote the sole problem that \(\hat c\) did not solve by: $$ \hat p \in P. $$
Now we must ask ourselves where have we been inefficient in terms of putting the data of the question to use. There are exactly two places:
Considering inefficiency 2, note that \(P^{(2)}\) carries some additional structure. Specifically, it has 6 distinguished 5-element subsets, one for each \(p \in P\): $$ Q_p = \{ \{p, q\} ~|~ q\in P, q \ne p \} \subset P^{(2)} $$
A natural way to put this extra structure to work is to study the behaviour of: $$ f(p) = \sum_{x \in Q_p}\|\nu^{-1}(x)\|. $$ Our hypotheses make it easy to evaluate \(f\) in two different ways: the double-counting trick again of course! On the one hand we have: $$ f(p) = \begin{cases} 5M + 1 & \mbox{ if } \hat x \in Q_p,\\ 5M & \mbox{ if } \hat x \not\in Q_p,\\ \end{cases} $$ because each problem pair in the 5-element set \(Q_p\) contributes \(M\) to the sum defining \(f(p)\), except for \(\hat x\) which contributes \(M+1\). On the other hand we have: $$ f(p) = \begin{cases} 3a_p + 1 & \mbox{ if } p \neq \hat p,\\ 3a_p & \mbox{ if } p = \hat p, \end{cases} $$ where \(a_p\) is the number of contestants who solved problem \(p\), because each contestant who solved \(p\) contributes 3 to the sum except for \(\hat c\), who contributes 4.
We have essentially arrived at the contradiction: \(f\) is overdetermined. Choose \(p, q \in P\) such that:
The above is of course just one possible solution. Prior to posting the above, I discussed this question with Ben North and he came up with a beautiful, different solution which I sketch below (actually I've slightly modified his solution but I believe I have retained its essence; all mistakes mine etc.). He begins similarly and also establishes the result by obtaining a contradiction under the hypothesis that all contestants solved 4 problems except for one who solved 5. The key difference in Ben's solution is that he double counts, not just over \(Q_p\), but also over its complement in \(P^{(2)}\). This provides both upper and lower bounds for \(a_p\) as follows: $$ 3a_p - 2\|C\| \in \begin{cases} \{0, 1\} & \mbox{ if } p \ne \hat p,\\ \\ \{1, 2\} & \mbox{ if } p = \hat p.\\ \end{cases} $$ He then observes that the integrality of \(a_p\) is compatible with the above only if: $$ 3a_p = 2\|C\| + 1, \mbox{ for } all ~ p \in P. $$ The contradiction is then obtained since we have: $$ \sum_{p\in P}a_p = 4\|C\| + 2, $$ but this sum represents the total number of solutions obtained, and so should be congruent to 1 modulo 4, since every contestant contributes 4 solutions except for \(\hat c\) who contributes 5.
I am grateful to Ben, not only for sharing this alternate solution, but also for making several suggestions which improved the exposition of my own.
Some day, I must get round to generalising this question. E.g., for an arbitrary number of problems, which rational numbers analogous to \(\frac{2}{5}\), and constraints analogous to \(C_6 = 0\), make for interesting results.
Incidentally this result is a special case of the formula expressing the intertwining number of two representations of a compact group in terms of the \(L^2\) inner product of their characters: we pair the trivial representation with the representation of \(G\) on the set of complex-valued functions on \(X.\)
Judging by (a frequentist's) expected score according to the data, the "hardest" problems were:
Let \(n\) be a positive integer. Consider $$ S=\{(x,y,z) : x,y,z \in \{0,1,\ldots,n\}, x+y+z > 0\} $$ as a set of \((n+1)^3 - 1\) points in three-dimensional space. Determine the smallest possible number of planes, the union of which contains \(S\) but does not include \((0, 0, 0)\).
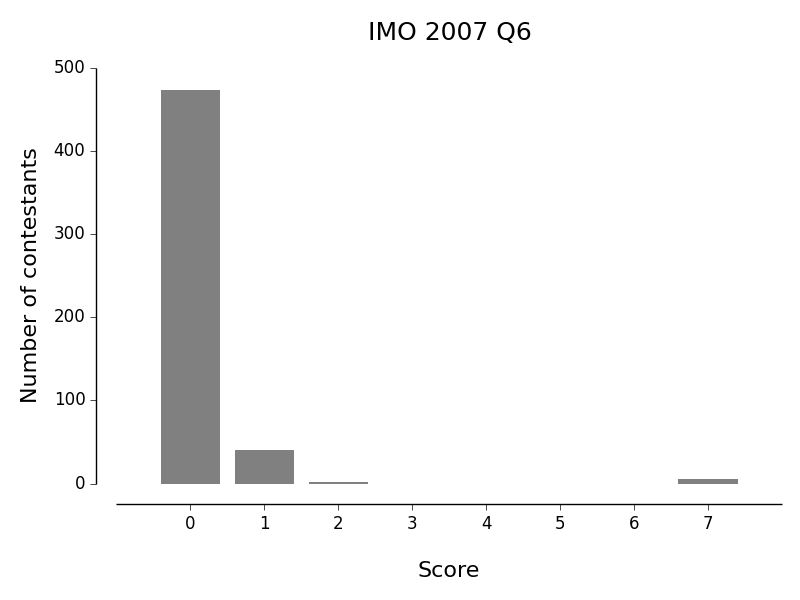
In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.
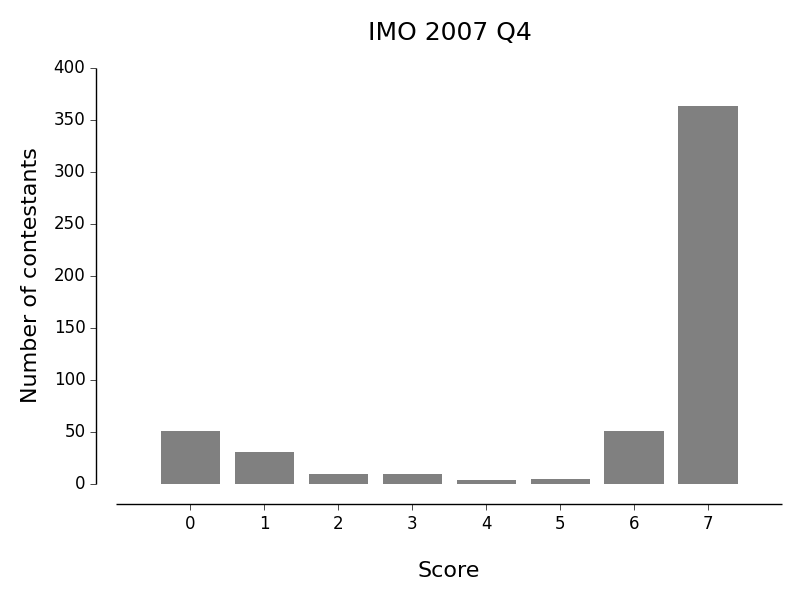
A magician has one hundred cards numbered 1 to 100. He puts them into three boxes, a red one, a white one and a blue one, so that each box contains at least one card.
A member of the audience selects two of the three boxes, chooses one card from each and announces the sum of the numbers on the chosen cards. Given this sum, the magician identifies the box from which no card has been chosen.
How many ways are there to put all the cards into the boxes so that this trick always works? (Two ways are considered different if at least one card is put into a different box.)