
A nice view is a great excuse to stop and catch your breath
Mining the Strava data
The cycling bug
Recently I was bitten (or at least nibbled) by the cycling bug. For several weeks I spent most mornings inching slowly up one side of a hill and then hurtling complacently down the other. Like many others, I found that my enjoyment of this somewhat Sisyphean exercise was greatly enhanced by tracking my efforts using Strava.
Strava provide an app that uses the GPS receiver in your phone (or other device) to record your location every few seconds for the duration of your cycle. Furthermore they allow you to upload this data to their servers and compare your performance with that of other athletes. They even provide an API that makes it easy to download others' data. Data points have components for latitude, longitude, altitude, time and distance travelled (from a designated start), speed, and gradient information.
I like playing with data and I spent many minutes on my cycles imagining what sorts of applications I might be able to find for Strava's repository of sweat and toil. Amongst the questions that I thought it might be interesting to attack are the following:
- For mountain routes, can we quantify the relationship between speed and gradient?
- Assuming 1, can we infer the gradient (and hence, by integration, altitude) series of a route using only the series of speeds?
- For city routes, can we infer the location of traffic lights / road junctions by looking for locations where significantly-many cyclists stop?
- Assuming 3, can we detect which cyclists obey the traffic laws?
- Can we quantify (or even detect) the effect of particular cycling gear (e.g., bike / shoe / cleat ...)?
- Can we detect any forms of cheating (e.g., abnormal velocity resonse curve to gradient)?
In this mini-post I'll discuss question 1 and explain how with even the simplest possible analysis, it is possible to obtain some positive results. (With more work I believe some very interesting results could be obtained; I may return to carry out more sophisticated analysis.)
My guess is that positive results could also be obtained at least for questions 2 – 4. I'd be interested to hear from anybody else who has carried out similar investigations. So far (apart from Strava Labs's heatmap) I have only been able to find one other account in a similar spirit.
Col du Tourmalet, L'Alpe d'Huez, and of course, Stocking Lane
Amongst the services that Strava provides is access to a vast database of (user-created) cycling routes which it refers to as segments. I decided to concentrate my analysis on three segments and picked what are probably the two most iconic climbs of the Tour de France: The Col du Tourmalet (in the Pyrenees) and L'Alpe d'Huez (in the Alps) as well as my local mini-climb here in Dublin, colloquially referred to as Stocking Lane. The table below gives summary stats:
Each time a person cycles one of these segments and uploads the tracking data to Strava, a segment effort is created. I used Strava's API to download all the publicly available segment efforts for each of these segments. The data needed cleaning so I carried out some simple data cleaning to remove inconsistent / obviously wrong / suspicious-looking data. I had enough data points that I could afford to adopt a rather conservative better-safe-than-sorry approach and threw out quite a few points (especially for the first two segments). I ended up with a dataset described by the table below table:
| Segment name |
Segment efforts before cleaning |
Segment efforts after cleaning |
Data points after cleaning |
| Col du Tourmalet |
2,206 |
686 |
1,722,778 |
| L'Alpe d'Huez |
5,808 |
1,778 |
4,509,180 |
| Stocking Lane |
4,605 |
3,489 |
2,098,640 |
I then aggregated the data points for all segment efforts, and generated various charts so that I could peek at the raw data for each segment. For example, the following charts are relevant for the question of relating speed to gradient:

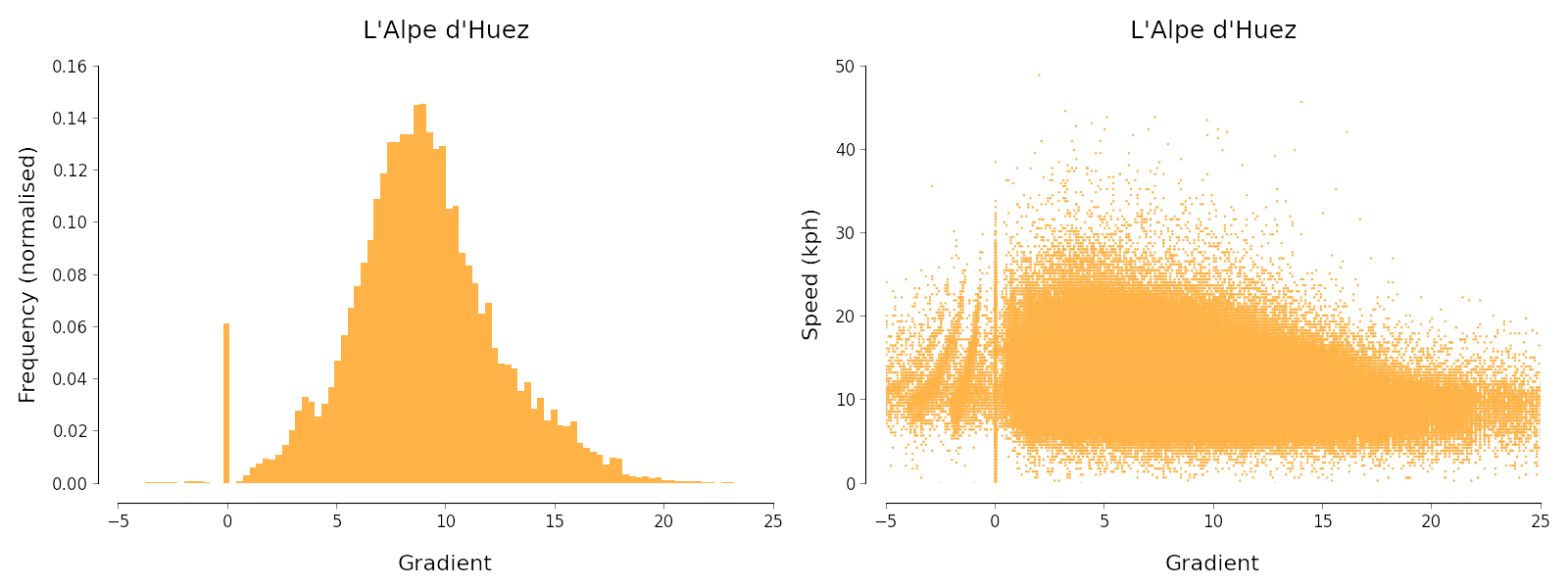
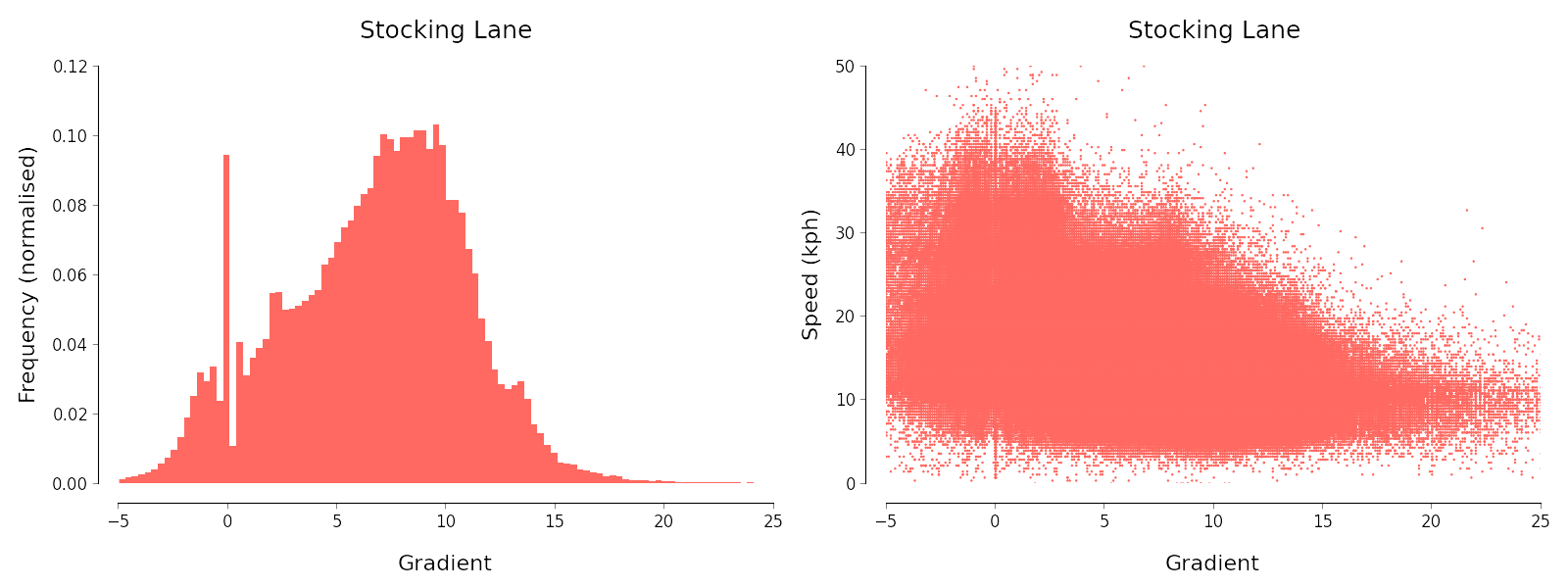
They show that even after my cleaning, various artefacts remain in the data which are almost-certainly the result of minor bugs in Strava's calculations. The most stark is the fact that gradients near 0 seem to be rounded to precisely 0. Nevertheless, the data look reasonable on the whole.
Speed as a function of gradient
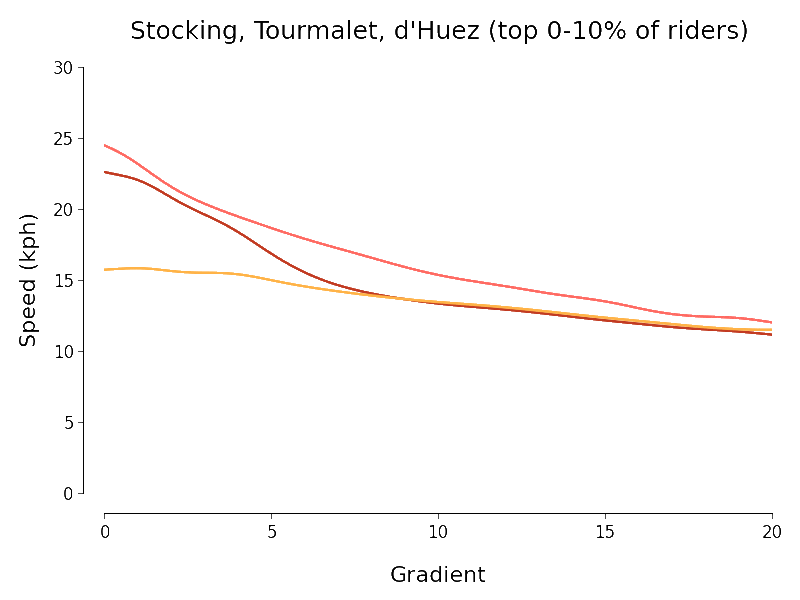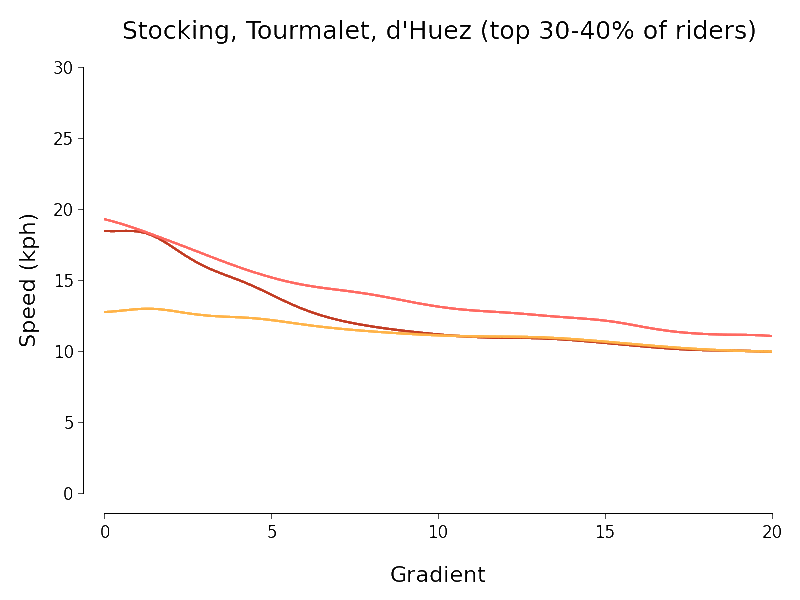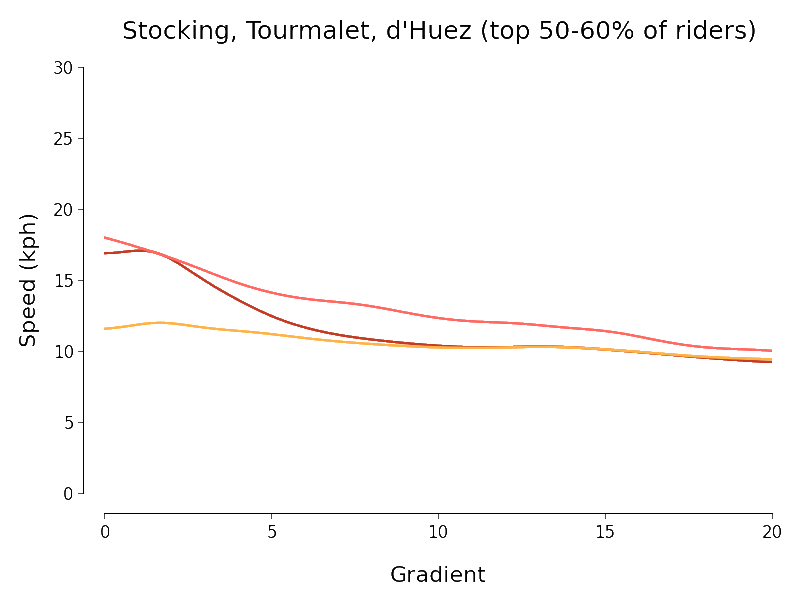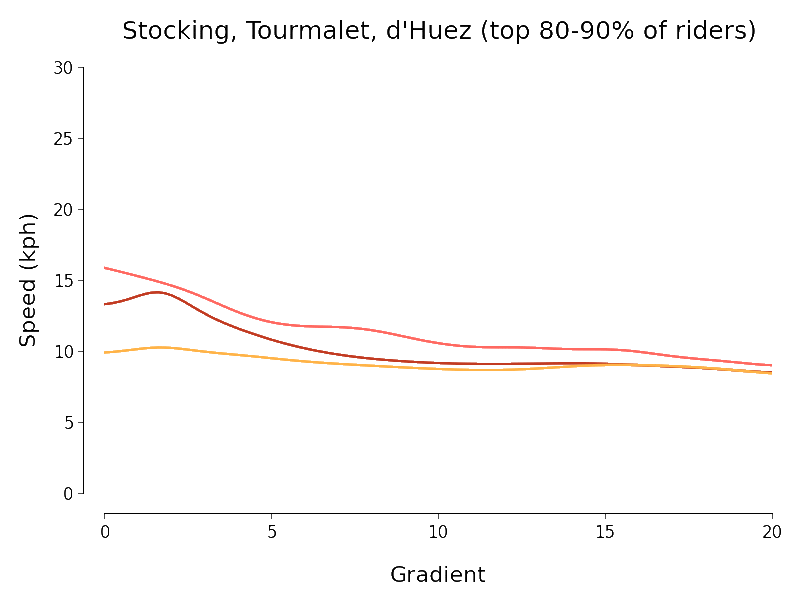
I set myself the goal of quantifying the intuitive downward trend in speed that we see in the scatter plots as gradient increases. To do this I experimented briefly with scikit-learn's SVR but ended up using simpler kernel regression (with Nadaraya-Watson estimator for Gaussian kernel) to investigate. Because there is a huge variation in mountain cycling ability I chopped each of my three datasets up into ten deciles (according to the number of segment efforts) and separately regressed speed against gradient for each piece. The chart below expresses the results I obtained (using the same colour scheme as the charts above):
Interpreting the regressions
I always like it when I manage to get a dataset to talk and so I find the above results somewhat pleasing. The following points approximately summarise my thoughts when I look at the above chart:
- At least at first sight, the Col du Tourmalet and Stocking Lane results look plausible but not really those for L'Alpe d'Huez.
- There is a pleasing agreement between the results of the regressions for the Tour de France routes at least for gradients of about 7% or more (independent of the decile).
- We should be especially careful interpreting the results outside the regions where most of the data points lie. In particular the histograms above show that most of the data points for the Tourmalet and Huez lie between gradients of 5 and 15%.
- By aggregating data points from all segments and ignoring their time components, I am not paying attention to the time-dependent nature of a cycle journey. For example, it is
likely that a person will cycle a 15% gradient towards the end of a climb more slowly than the 15% near the beginning. It would not be too hard to posit and fit a time series model for human cycling behaviour that could account for this and might yield very interesting results.
- I expect L'Alpe d'Huez actually has a more-nearly constant slope than its histogram above indicates. If this is the case, a noisy estimator for gradient would yield the slightly surprising-looking results we have obtained in which the speed-gradient curve looks too flat.
- I used Strava's grade_smooth and velocity_smooth series for my analysis. In fact I also have the raw GPS latitude and longitude (but not altitude) values as well as a distance (often from an odometer, I believe) and time values. I may thus may be able to use simple filtering techniques from signal analysis to get much less noisy estimates for the gradient and speed time series. Indeed the problem seems to be an instance of a classic application of the Kalman filter and it looks Strava have used much simpler techniques to generate their grade_smooth and velocity_smooth series. Additionally I may be able to enhance data quality further by using data from the Google Elevation API.
A power equation
It would be nice to be able to connect the data with physics. Again I won't pursue this but I believe it could be done fairly easily along the following lines. Suppose we could magically track the following four quantities:
- Rate of change of kinetic energy, PT
- Rate of change of potential energy, PV
- Rate at which the air drag force does work, PD
- Rate at which the body metabolises fat and sugars to liberate biochemical energy, PB
For a cyclist cycling up a hill of constant gradient in a steady state, the following should be a good approximation:
$$P_T = 0$$
$$P_D + P_V - P_B = \mbox{const}$$
Thus if there is no wind, if v is the speed and if t (for tan(x)) is the gradient then remembering the formula for drag force we obtain:
$$v^3 + \frac{a}{1 + t^{-2}}v - b = 0$$
for positive constants a, b. This cubic equation has negative discriminant and thus a unique real root which yields the steady state speed as a function of the gradient. This is really only worth mentioning because it says that v should be a function of the square of t. Perhaps we would have been better off regressing against \( t^2\) above rather than \( t\)?
Lastly, regarding the constants a, b. These are determined by the mass of the cyclist, the acceleration due to gravity, the density of air, the cross-sectional area of the cyclist (in the direction of motion) and the drag coefficient. The first three quantities are easily obtainable and the latter two may be obtained from literature such as this paper. I expect that with sufficient effort it should be possible, for example, to back out what power a cyclist was outputting using the Strava data.
Source code
For any interested souls, here is a link to the source I used to carry out the above.







