12 piece wooden puzzle

A 3D printing puzzle

A wooden puzzle

Back in 1998 when I was in Taiwan I bought a nice little wooden puzzle. The point of the puzzle is to disassemble/reassemble a cube like the one pictured above. It caught my eye because it had the same design as a puzzle that a friend from back home in Dublin had. I had often admired my friend's puzzle but never knew where to get one (he had bought his while skiing in Andorra). These were the early days of online commerce and it was not so easy to get your hands on things. As a result I didn't hesitate before snapping up the puzzle when I happened across it in the gift shop in Taipei.

A beautiful building in Liberty Square in Taiwan

Fast forward 10 years to 2008. A different friend was round at my apartment and took an interest in my nice Taiwanese puzzle. He was having trouble solving it so I encouraged him to take it home. Little did I realise. I was not to see that wooden puzzle again for almost 3 years (and btw he still hadn't solved it when he finally returned it!).

Towards the end of those 3 years, i.e., a few months ago, I began to get interested in 3D printing. The idea to have a replacement of my missing wooden puzzle made occurred to me. Although I lacked the puzzle, I had typed the coordinates of all the pieces into my computer about 10 years before (for a 3D rendering project I was working on). It had been pretty painful work typing up all those coordinates so I had always been careful not to lose them. Now, finally, they were going to be really useful!

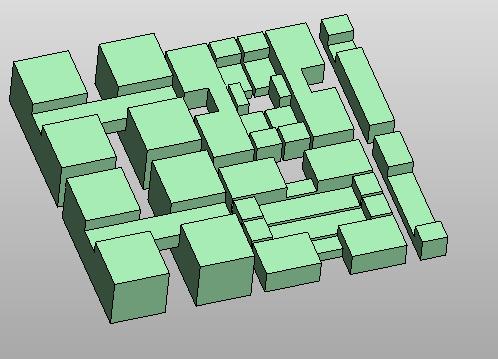
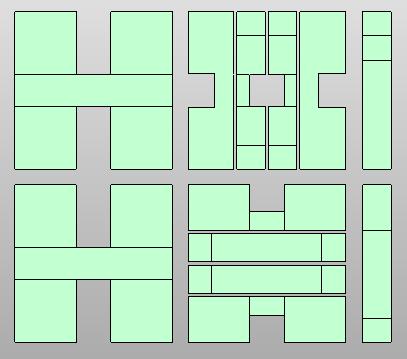
Two views of the 12 pieces of my virtual puzzle

The idea that I could turn these simple lists of coordinates into a physical 3D object hugely appealed to me. Also, I had (indeed I still have) some other more substantial 3D printing projects in mind and this simple puzzle request would give me data on the accuracy of the process. In other words, I thought having the puzzle made would be a good test run. Plus, I'd have my puzzle back!

3D Printing

We live in a brave new world: 3D printing is here! I for one find the idea of being able to print 3D objects extremely exciting.

There are a number of techniques including selective laser sintering, fused deposition modeling and DLP/stereolithography (this last term is a little loose). Each of these builds up the 3D model as a series of relatively thin (usually ~0.1mm) 2D slices and as such are additive processes in contrast to more traditional machining methods. There are a number of firms making the various types of 3D printing machines including ZCorp, Eos, Stratasys and Objet. There are even two open source 3D-printing possibilities, that are financially withing range of many a sufficiently interested hobbyest: Makerbot and Reprap. Finally there are several web-based firms which offer to 3D print a model on an industrial machine and post the results back to you. These firms include:
i.materialise using many machines
Ponoko using ZCorp SLS machine machines (Ponoko also offer excellent 2D laser cutting services)
Sculpteo using ZPrinter 650 by ZCorp and Formiga P100 by Eos machines
Shapeways using Stratasys FDM 400mc and Objet Eden 500(V) machines
Each of these websites/machines accept various 3D file formats. The most widely accepted, and also the simplest, file format seems to be the so-called Stereolithography file format (extension STL). I decided to supply my pieces in this format and wrote a simple python script to convert my old lists of coordinates into this format as well as to tidy up the 3D geometry in various ways (orient normals consistently, introduce clearance space between the pieces, fix T-junctions etc.). The source code, which looks like this: 


  from geometry import *
  from collections import defaultdict
  import sys


  #...


  piece = Solid(sys.argv[1][:-3] if sys.argv[1].endswith('.3d') else sys.argv[1])
  piece.read_from_3d_file()
  piece.fix_normals()
  piece.fix_T_junctions()
  piece.create_clearance(0.5, 25)
  piece.place_on_z_plane(int(sys.argv[2]), int(sys.argv[3])) # Sorry, horrible hack!
  piece.write_to_stl_file()
is available here, the raw input files are available here and finally the output, ready for 3D printing, is available here.

Finally, with my data ready and in the right format, I uploaded my STL file to i.materialise. I was curious to see what their "alumide" material (a mixture of polyamide and aluminium powder) would be like so I requested to have my puzzle printed as alumide using selective laser sintering. I was pleased with the results:

Two views of the 12 pieces my replacement alumide puzzle

Accuracy of the 3D-printed alumide puzzle

As I mentioned above, one of the reasons for having the puzzle made was to see how accurate an instance of the 3D printing process was. Fortunately the puzzle is an easy object to measure because every surface point lies in a plane parallel to a (Euclidean) coordinate plane. I thus decided to use a digital caliper to make measurements of the pieces of the puzzle. The caliper I used to make the measurements has a precision of 0.01mm and claims to have accuracy to this scale also. I doubt this but I am reasonably confident that it has at least 0.1mm accuracy based on a few tests (and I expect better). Based on 41 measurements I found a sample mean and standard deviation error of 0.24mm and 0.11mm respectively. I also found that all errors were positive meaning that they were due to too much material being deposited; no measured dimension was too small. (Incidentally this means that if you are ambivalent as regards errors caused by too much or too little material being present, you should shrink your model appropriately by ~0.24mm to try and achieve zero average signed mean and 0.12mm average absolute mean.)

The alumide puzzle assembled.

For the sake of completeness I might as well provide the table of measurements I took.
Measurements

Record ID Piece Normal direction Plane 1 location Plane 2 location Theoretical distance Measured distance Error
1 1 z 0 19.5 19.5 19.67 0.17
2 1 z 0 19.5 19.5 19.73 0.23
3 1 x -25 25 50 50.29 0.29
4 1 x -25 25 50 50.24 0.24
5 1 x -25 -5.5 19.5 19.79 0.29
6 1 z 8.5 14.5 6 6.56 0.56
7 1 y -25 25 50 50.24 0.24
8 1 y -25 25 50 50.22 0.22
9 1 y -5 5 10 10.32 0.32
10 2 z 0 19.5 19.5 19.9 0.40
11 2 z 0 19.5 19.5 19.86 0.36
12 2 x -25 25 50 50.25 0.25
13 2 x -25 25 50 50.29 0.29
14 2 x -25 -5.5 19.5 19.76 0.26
15 2 z 8.5 14.5 6 6.45 0.45
16 2 y 80 30 50 50.2 0.20
17 2 y 80 30 50 50.2 0.20
18 2 y 50 60 10 10.33 0.33
19 3 y 80 30 50 50.16 0.16
20 3 y 60 50 10 10.21 0.21
21 3 z 0 9 9 9.14 0.14
22 3 x 45.5 54.5 9 9.34 0.34
23 3 x 45.5 54.5 9 9.42 0.42
24 5 x 30 80 50 50.21 0.21
25 5 x 30 37.5 7.5 7.54 0.04
26 5 x 72.5 80 7.5 7.55 0.05
27 5 y -0.5 -9.5 9 9.28 0.28
28 5 z 0 4 4 4.08 0.08
29 7 y 80 30 50 50.15 0.15
30 7 y 49.5 30 19.5 19.64 0.14
31 7 z 0 9 9 9.32 0.32
32 7 x 44.5 30 14.5 14.66 0.16
33 9 x 30 80 50 50.09 0.09
34 9 y -10.5 -25 14.5 14.63 0.13
35 9 z 0 9 9 9.36 0.36
36 11 x 85.5 94.5 9 9.28 0.28
37 11 y 25 -25 50 50.21 0.21
38 11 z 0 9 9 9.08 0.08
39 12 x 85.5 94.5 9 9.3 0.30
40 12 y 80 30 50 50.17 0.17
41 12 z 0 9 9 9.16 0.16
Avg 0.24
Std 0.11
Min 0.04
Max 0.56

Final words on the 12 piece puzzle

I thought I'd finish with a brief appeal for information. In the course of the above I began to wonder about the origin of my puzzle. I would be interested to know when/where it was invented. I was unable to determine this after a few hours of googling but I think it likely some facts about the origin are known. I did come across this page where it is claimed that the puzzle dates from at least the 19th century (incidentally there is also a clear solution to the puzzle given on that page).

I also discovered that there is an extremely extensive database of mechanical puzzles assembled by Jerry Slocum known as the Slocum collection but I could not find my puzzle in the online database. Apparently a classic puzzle reference book is Prof. Hoffman's "Puzzles old and new", 1893 so it would be interesting to see if my puzzle is mentioned there but the book is hard to come by. My guess is the puzzle dates from 19th century Europe but it seems that puzzles have been very popular in Japan for a long time where the keyword is "kumiki" apparently meaning "joining wood together".